Results

  We have implemented the ideas above in portable ANSI C. Interprocessor communication is through a simple API of our own design which, in turn, may directly use Unix sockets, or many of the open or vendor-specific communication libraries, e.g., MPI, NX, etc. The results here are for a cluster of 16 200MHz Pentium Pro systems running Linux each with 128MB of memory and a 1GB EIDE disk partition devoted to out-of-core scratch space. The peak performance of this system is 200Mflops/processor, but in practice, a highly optimized vector of in-cache, gravitational interactions runs at approximately 86Mflop/processor. The communication system is very modest - consisting of a single 100baseT ethernet switch, delivering a bi-directional bisection bandwidth of 80MB/s and latency of to user-level code. The entire system is constructed from mass-market commodity parts and is extremely cost-effective, with a total purchase price in autumn 1996 of under $60000.

All benchmarks reported here are for uniformly distributed collections of particles. The tree has a maximum terminal occupancy, m=3. We simply have not had time to run highly non-uniform cases but we believe, based on our in-core results, that the non-uniformities typical of astrophysical systems will not introduce significant new overheads. The runs involved between 1000 and 1350 monopole interactions and approximately 150 MACs per body. Higher order moments could be employed without substantially changing the code, but the bandwidth vs. operation-count tradeoffs need to be carefully considered. Measured times are for an entire, realistic timestep, i.e., they include sorting, tree building, force evaluation and time-integration. In the parallel case, they do not include redistribution of particles to processors, but we expect this to be a small additional overhead which will be substantially offset by the fact that the particles begin subsequent timesteps almost sorted.

Figure 4 shows overall performance of the system for a fixed size problem (5 million bodies) and for a problem that grows with the number of processors ( bodies). The abscissa has been scaled to factor out the average work per processor, so that the departure from horizontal indicates parallel overhead in the fixed-size case. Note, though, that for a fixed size problem, as we add processors, more and more of the data fits in memory, so the observed ``super-linear'' speedup is not unreasonable. The largest system is an 80 million body model which took 5363 sec/timestep on 16 processors. The single-processor, 5 million body model took 4346 sec/timestep. In contrast, our in-core code integrates a 500000 body model with comparable accuracy in 378 sec/timestep, so the net performance cost of using disk achieve a factor of ten increase in dynamic storage capacity is in the neighborhood of 15%.

 

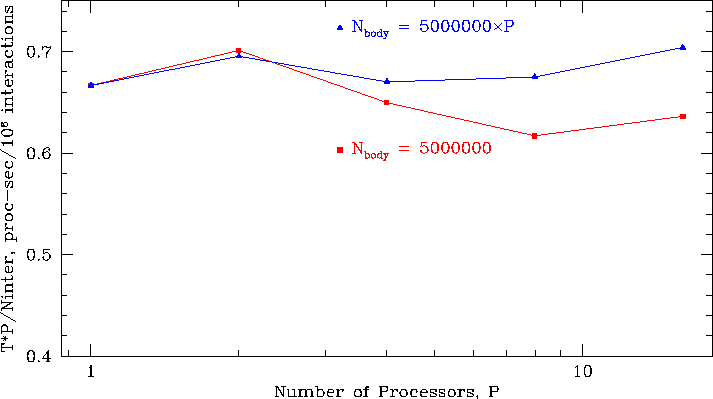
Figure 4:   Scaling behavior up to 16 processors for a fixed size problem (5 million bodies) and a problem that grows with the number of processors ( bodies).

The Linux kernel maintains a ``buffer cache'' of disk pages in OS-controlled memory which grows and shrinks in opposition to user-memory. This feature significantly improves normal operation, but makes benchmarking difficult because if we restrict ourselves to a small working set, and then ask to move pages to and from disk, there is a very good chance that the kernel will find the pages in a buffer cache and not need to query the disk controller at all. The net result is that wall-clock times for I/O operations are often far less than one might expect based on hardware disk latencies and bandwidths, and they are strongly influenced by the vagaries of the kernel's buffer cacheing policies and the size of the system's DRAM. Rather than attempt to isolate these effects, we simply report the number and size of pages swapped, with the assumption that this provides a lower bound on performance.

Figure 5 shows paging behavior for a simulation with 1 million bodies on a single processor. The model requires about 72 MB of storage altogether. Runs were made with different combinations of the page size and the number of in-core pages. The amount of swapped data is flat over a large range of in-core sizes, and falls dramatically as the in-core size approaches the size of the entire data set. Furthermore, once the number of in-core pages exceeds about 200, there are diminishing returns in making it larger, allowing one to increase the page size instead. Thus, one can amortize disk latency as long as the in-core memory exceeds about , i.e., only 3MB of DRAM is needed to effectively run out-of-core with a commodity EIDE disk. It is tempting to try to fit this in cache, but unfortunately it is almost impossible to get explicit control over cache behavior on modern processors.

 

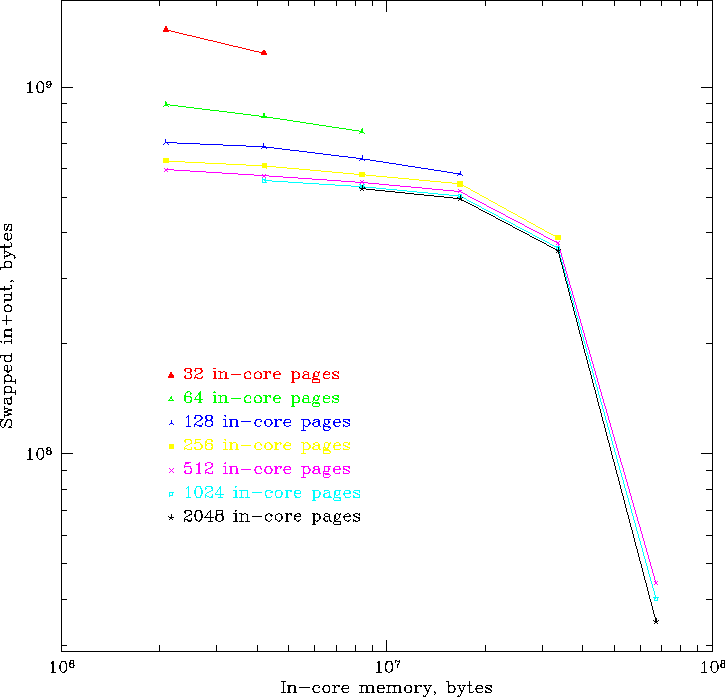
Figure:   Aggregate swapped data vs. in-core storage for a 1 million body model and various parameter choices of page size and number of in-core pages.