In the friends of friends (FOF) method of halo finding [5],
one specifies a linking length, 
, and identifies
all pairs of particles with a separation of or less.
Such pairs are designated friends, and halos
are defined as sets of particles that are connected by
one or more friendship relations, i.e., friends of friends.
The linking length is usefully parameterized
as a density, and following [12],
we define a density threshold:
where 
is the average particle mass in the simulation.
That is, 
is the density
of a sphere of radius containing two average mass particles.
In regions where the density is greater than
, particles will tend
to be closer together than , and will be linked together
in the FOF method.
Notice that the mechanics of the FOF method do not involve density,
but the effect of the method is to identify density peaks above
the threshold .
A second parameter in FOF is the minimum
number of particles, 
, in a halo.
The purpose of is to reject spurious halos -- i.e.,
groups of friends that do not form persistent objects in the
simulation.
Chance associations involving larger numbers of particles
are less likely than those involving fewer, so
by setting sufficiently large one hopes to
avoid most spurious halos.
Figures 1 and 2 show two sets of
results, using = 10 and = 30, from FOF on Model 3.
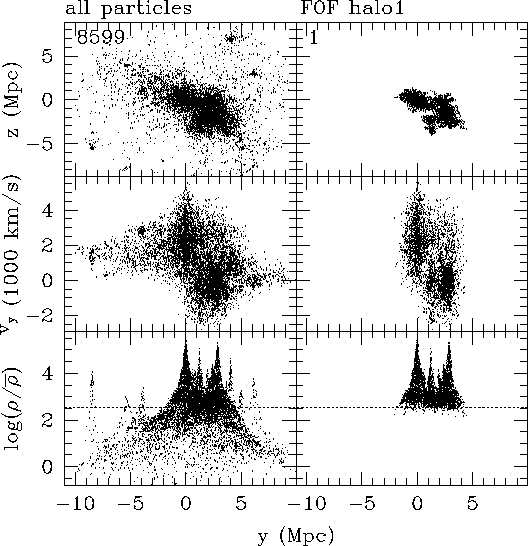
Figure:
Particles in Model 3, and the central halo found by FOF
in this model. These panels illustrate the difficulty of graphically
representing data that samples a six-dimensional space (three position
and three velocity components). In each panel
the horizontal and vertical axes each represent one degree of freedom,
and each particle contributes a single dot.
In all panels, the horizontal axis is an arbitrary spatial coordinate
(in this case, the y-coordinate).
The panels on the left show all of the particles in the model;
those on the right show the particles
in the single most massive halo found by FOF.
The upper panels show particle positions, projected
into the spatial y-z plane.
The middle panels show the same spatial coordinate
and one velocity coordinate.
The lower panels show the density
(as calculated by IsoDen according to
equation 2;
see Section 4)
and the same spatial coordinate. The lower panels emphasize the
spatial variation and complex hierarchy of densities. It is clear
from the lower right panel that the FOF method has failed to identify
some of the substructure in the model, combining several distinct halos into
a single halo.
The horizontal line in the lower panels indicates
the value of corresponding to the used for FOF.
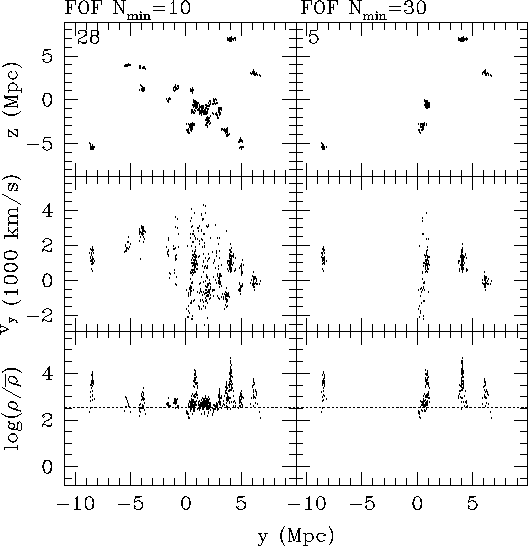
Figure:
As Figure 1, showing
halos other than the central halo, as found by FOF with
= 10 (on the left) and = 30 (on the right).
The number of halos in each case is indicated at the top left.
The large spread in the velocity coordinate in the middle panels
indicates that even though some groupings of particles have high spatial
density, they may not be gravitationally bound, and hence do
not constitute a persistent object in the simulation.
Thus, the middle panels suggest that many of the selected halos on the
left, and at least one of those on the right are spurious.
The lower and upper panels, however, indicate likely structures on the left
(identifiable with = 10), which are rejected by the choice of
= 30 on the right.
Thus, neither value of is entirely satisfactory.
These figures demonstrate two problems with FOF: joining halos together,
and poor distinction of small halos from noise.
The first problem is that at the center of the cluster,
FOF finds one large halo which is clearly composed of
several distinct halos.
This is because everything in a region
where the density is above is joined into a single halo,
whether or not the region includes objects which are distinct at
some higher density -- a problem first noted by [3].
From the density plots it is seen that there is no
value of which will distinguish the halos in
the high density region without missing some
of the lower density halos.
The second problem is the arbitrariness and ineffectiveness of the parameter.
In our test,
the value of = 10 is too small,
since many of the small halos found
have high internal velocity scatter,
and hence are not bound
(c.f. figure 2 left middle panel)
At a higher of 30, (figure 2 right panels)
most of the spurious
halos are rejected, but one remains, and in addition several
real (but small) halos have been rejected.
